每个面对的相同问题就是,如何准确的衡量信息安全风险。在多数情况下,并没有足够的信息可以用于衡量风险,不过现在我们可以根据已知的数据泄漏事故来得出一些结论以及如何应对信息安全的教训。
衡量风险
与某个事件相关的风险通常是指这个事件可能造成的平均损失,这也是预期年均损失(ALE)风险管理方法的基本依据。信息安全领域的人基本上都知道ALE方法,ALE甚至是CISSP CBK(信息系统安全认证)的知识。但是,几乎没有人实际使用过这种方法。
ALE方法告诉我们可以通过将事故发生造成的损失与事件发生的可能性相乘来计算一个事件的风险。举例来说,某个事件可能造成1百万美元的损失,而每年发生的几率是千分之一,那么这个事件的风险就是每年1000美元,将1百万乘以千分之一。
在信息安全领域使用ALE方法的最大问题就是,我们通常都不知道具体事件将造成的损失以及事故发生的可能几率。可能所有都存在可能被利用的漏洞(安全研究人员尚未发现),但是这些漏洞明年被发现的几率是多少呢?如果发现了某个漏洞,那么如何准确计算攻击者利用这个漏洞所造成的损失呢?这些问题都是很难解决的问题,因此在信息安全领域,传统的风险管理方法都是很有限的。
而在数据泄漏发明,却存在很多可用的数据。开放式软件基金会(OSF)对2000多起数据泄漏事故进行了追踪调查,从他们的数据中,我们可以发现很多有趣的结论,下面就是自2006年1月起发生的数据泄漏图示:
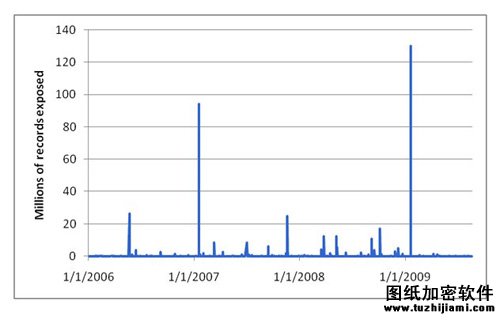
并不难看出图中的数据泄漏事故发生次数的规律,但是如果我们取出这些数据的对数,会发现更有趣的现象,也就是正态曲线,我们有时也称为“钟形曲线”。更有趣的是,数据泄漏事故的大小的对数也刚好形成正态分布,平均偏差为3.4,标准偏差为1.2。下图将数据泄漏事故大小与正态分布图进行了对比:
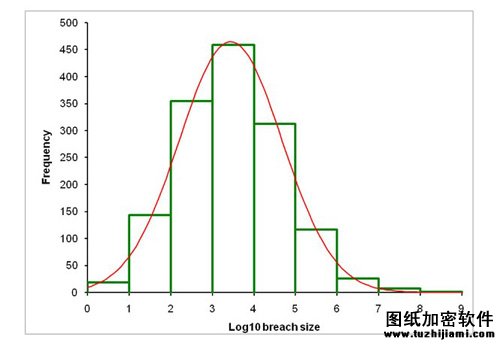
这些数据泄漏事故确实存在某种规律,它符合所谓的对数正态分布,虽然数据泄漏次数本身不符合正态分布,但是数据的对数符合正态分布。
解析这些信息
知道数据泄漏事故的大小符合对数正态分布能够告诉我们一些信息,但是不能告诉我们所有信息。
知道数据泄漏事故的大小符合对数正态分布并不能帮助我们预测下一次数据泄漏将要发生的时间,以及当发生数据泄漏时将会有多少信息被泄漏,但是它能够帮助我们预测几周或者几个月内数据泄漏的发生几率,能够让我们预测大约多久会发生一次泄漏1百万甚至更多数据的事故,或者让我们预测明年至少会发生一次泄漏1百万多条数据的泄漏事故,这是非常重要的信息。
数据泄漏事故的大小符合对数正态分布甚至还可以告诉我们数据泄漏发生的方式。 当我们观察到的数据是拥有随机分量的一个或者多个值相乘的结果时,我们就得到了对数正态分布图。因为这是真实的,我们很自然就会想到数据泄漏是由于多个安全机制的一个机制发生的错误而造成的,这些安全机制的影响结果相乘就得到了数据泄漏的总损失。
这确实是个合理的模型,但是对数正态分布在很多其他情况也会发生,有些也不能这样解释。特别是,以下列出的值符合对数正态分布,但是在这些情况下并不能肯定其中存在相乘的影响发生:
o 在矿石中提取金和铀
o 细菌食物中毒的潜伏期
o Alzheimer疾病起始年龄
o 洛杉矶的大气污染数量
o 鱼种类的数量
o 冰淇淋中冰晶的大小
o 电话谈话中用词的数量
因此,认为数据泄漏是由于一个或者多个安全错误的影响力相乘的结果实际上也许是个正确的观点,也存在这样的情况,出现的对数正态分布图似乎与这种模型不存在有意义的关联。
Benford定律
数据泄漏大小似乎也符合Bedford定律。
符合Benford定律的数据的起始数字并不太可能,较小起始数据比较大数据更据可能性。从1开始是最普遍的,而且发生机率为30%。从9开始是最少的,几率为5%。
并不是所有数据都符合Benford定律,但是数据泄漏的大小确实符合,如下图所示:

由重复相乘所得到的数据比较符合Benford定律。为了验证这个的正确性,可以尝试追踪每年增长率为10%并且为期30年的投资。你会发现投资的值符合Benford定律。因为数据泄漏事故的大小同样符合Benford定于,这也让我们再次确定数据泄漏是由于一系列安全错误的结果相乘造成的结果。
利用这个信息
既然我们知道有些方面的数据泄漏是可以预测的,那么我们应该如何利用这些信息呢?其中一种方式就是衡量行业范围内为降低数据泄漏作出的改进的有效性。我们也许会看到数据泄漏事故大小的对数的平均偏差将从3.4降到3.0,如果真的是这样,那么我们就有证据证明作出的改进是有效的。
事实上,我们并没有太多关于安全事故(除数据泄漏外)的有效数据,但是也许其他事故的发生几率也符合对数正态分布,这有待以后研究。
我们从这些信息中可以得到的是,我们目前还无法使用传统的风险管理方法来管理现在数据泄漏问题,但是这些信息让我们得到了过去都没有发现过的信息。了解数据泄漏的发生形式是很好的第一步。
